In a crystalline solid, the atoms form an ordered lattice. Crystalline solids respond elastically to small deformations: When the applied strain is removed, the macroscopic stress, as well as the microscopic configuration of the atomic lattice, goes back to the original state. On the other hand, a material behaves plastically if it does not return to its original state. In general, plasticity only occurs when the deformation is sufficiently large.
Unlike crystals, amorphous solids, such as glasses, granular matter, gels, foams, and emulsions, have disordered particle configurations. How do amorphous solids respond to a small deformation? Can standard elasticity describe amorphous solids?
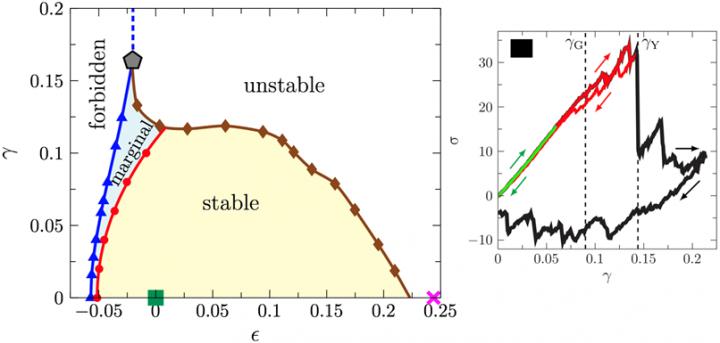
To answer this question, Dr. JIN Yuliang from the Institute of Theoretical Physics (ITP) of the Chinese Academy of Sciences, together with his collaborators, systematically studied the mechanical properties of amorphous solids using a numerical model system.
Even though macroscopic properties such as stress and strain are reversible upon releasing a small deformation, microscopic configurations can be irreversible. The work needed to switch between before- and after-perturbation configurations is infinitesimal. This kind of amorphous solid is called marginally stable and results from a so-called Gardner transition, as predicted recently by mean-field theory.
The researchers further established a stability-reversibility map of hard-sphere amorphous solids, which unifies mechanical behaviors including elasticity, plasticity, yielding, and jamming.
According to the stability-reversibility map (Fig. 1), an amorphous solid has two typical behaviors, which depend on the extent of volume and shear strains. In the stable region, the amorphous solid is truly elastic and reversible, just like crystals. In the marginally stable region, on the other hand, elasticity is unavoidably mixed with plasticity, even for infinitesimal deformations. A marginally stable amorphous solid is only partially reversible.
The study shows that a more complete elastic theory is needed – one that can correctly incorporate amorphous solids. It also provides important insights into the design of next-generation mechanical materials such as metallic glasses.

