Anybody who has ever seen a picture of a brain knows that it’s not a simple smooth oval; it’s more like a tangle of fat worms. But when researchers seek to predict and understand its physical and electrical behavior, they have to describe fields on that complicated shape and often use simplified geometrical models, such as an ellipsoidal shape, for that purpose. It’s not that they’ve never seen a brain before, it’s that the twists, turns and valleys of a brain’s surface substantially complicate the modeling of parameters on it.
For simulations involving brain geometries, errors can be generated by a process called segmentation, which essentially assigns pixels to particular matter, such as cerebrospinal fluid and gray or white matter. For pixels located at the physical interface between these regions, the decision to assign a particular label can generate errors for small contrasts, and these uncertainties can propagate in subsequent analyses.
Johann Guilleminot, assistant professor of civil and environmental engineering at Duke University, has developed a technique to overcome these obstacles. And he’s using it to help researchers model a wide range of objects, such as stresses within an individual’s arteries, the effects of transcranial magnetic stimulation on a brain, and the forces at work within surgically implanted 3D-printed orthopedic devices.
“In most works related to uncertainty quantification, brains are often approximated by ellipsoids and arteries are often approximated by hollowed cylinders, because the geometry and coordinate systems are easier to handle in terms of stochastic modeling,” Guilleminot said. “But as soon as you try to account for real-world, patient-specific objects, the usual techniques begin to fail. We’re providing people who need to model these complex shapes and their complex properties and behaviors the ability to do so efficiently on the fly.”
Guilleminot’s method has two parts. The first generates a complex virtual model of most any shape desired and technically operates in the same way from object to object. The second takes a set of application-specific characteristics—the properties at work within a titanium leg implant or the patient-specific tissue stiffness within an artery—and maps them onto the 3D model.
The result is not only a complex, realistic virtual model of the object in question, but also a range of behaviors that it might exhibit. By incorporating variability into the computations, the models provide a glimpse into a spectrum of responses an object might have to certain loads, stresses and strains—hence enabling better classification, design and prognosis.
“If you run the same experiment on 10 real titanium implants, all processed under seemingly similar conditions, you won’t get the same results every time,” Guilleminot said. “You get variability, up to 20%, and sometimes it’s a huge difference because it can impact the durability and performance of an implant over the first few years.”
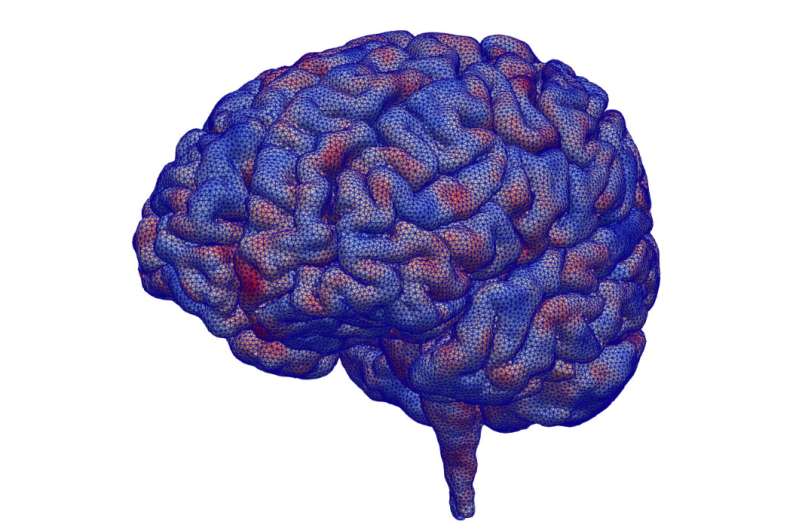
Guilleminot is helping get a more accurate and detailed view of the brain for researchers working with Transcranial Magnetic Stimulation (TMS), which applies electromagnetic fields from outside of the head to induce neural activity. In this image, blue represents geometrical perturbation inwards, while red represents geometrical perturbation outwards. By creating these virtual perturbations in brain models and solving them, Guilleminot can approximate and account for errors created during MRI scans.

Orthopedic surgical implants are often used to help heal and strengthen broken bones. Engineers are developing more complex shapes that help the bone grow into the implant and make the junction stronger, but the advanced geometry makes it more difficult to model stresses and strains on the device. In this image, the red and blue highlights show spatial fluctuations created by accounting for both geometrical features and the manufacturing process. This not only helps on the mechanical and clinical sides, but also provides a feedback loop on material processing.

This picture shows the average field of Von Mises stresses—a quantity that is typically used to asses failure of a structure—within a specific human artery. The field results from a coupling between the geometry, the material model and the way the statistical fluctuations are prescribed in the artery wall. The research could eventually underpin patient-specific simulations to help physicians develop non-invasive techniques for early diagnosis and identify potential pitfalls before performing medical procedures.
Ken Kingery, Duke University

